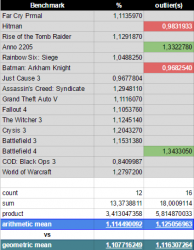
1^ case
Card1: 50 FPS in first game, 75 FPS in second game.
Card2: 75 FPS in first game, 50 FPS in second game.
Say you want to use Card1 as a reference.
Card1: 100% in first game, 100% in second game.
Card2: 150% in first game, 67% in second game.
Mean Card1: 100%. Geometric Mean Card1: 100%.
Mean Card2: 109%. Geometric Mean Card2: 100%.
Say you want to use Mean as a reference.
Card1: 80% in first game, 120% in second game.
Card2: 120% in first game, 80% in second game.
Mean Card1: 100%.
Mean Card2: 100%.
2^case
Card1: 40 FPS in first game, 50 FPS in second game, 60 FPS in third game.
Card2: 120 FPS in first game, 100 FPS in second game, 90 FPS in third game.
Say you want to use Card1 as a reference.
Card1: 100% in first game, 100% in second game, 100% in third game.
Card2: 300% in first game, 200% in second game, 150% in third game.
Mean Card1: 100%. Geometric Mean Card1: 100%.
Mean Card2: 217%. Geometric Mean Card2: 208%.
Say you want to use Mean as a reference.
Card1: 50% in first game, 67% in second game, 80% in third game.
Card2: 150% in first game, 133% in second game, 120% in third game.
Mean Card1: 66%. --> 100%.
Mean Card2: 134%. --> 203%.